
 | Смирнова Надежда Вячеславовна,учитель математики гимназия № 8 |
Вернуться к списку участников конкурса
1. Программно-содержательное конструирование стохастической линии в средней школе
2. Основные понятия теории вероятностей
3. Методические замечания: из опыта работы
4. Вероятностный граф – наглядное средство теории вероятностей
5. Модуль «Энтропия и информация» - метапредметность школьного курса Теория вероятностей
Введение
Современное общество предъявляет к своим членам довольно высокие требования, относящиеся к умению анализировать случайные факторы, оценивать шансы, выдвигать гипотезы, прогнозировать развитие ситуации, принимать решение в ситуациях, имеющих вероятностный характер, в ситуациях неопределенности, проявлять комбинаторное мышление, необходимое в нашем перенасыщенном информацией мире.
Наиболее эффективно эти умения и навыки позволяет формировать курс «Теория вероятностей и математическая статистика», о необходимости изучения которого в российской школе люди науки спорят на протяжении последнего столетия. В разные периоды становления Российского образования подходы к стохастической линии менялись от полного ее исключения из математического образования в средней школе до частичного и полного изучения основных понятий. Одним из основных аспектов модернизации российского школьного математического образования XXI века является включение теоретико-вероятностных знаний во всеобщее обучение. Стохастическая линия (соединение элементов теории вероятностей и математической статистики) призвана сформировать понимание детерминированности и случайности, помочь осознать, что многие законы природы и общества имеют вероятностный характер, реальные явления и процессы описываются вероятностными моделями.
Являясь студенткой Ярославского государственного педагогического университета им.К.Д. Ушинского, под руководством профессора В.В. Афанасьева я достаточно активно занималась именно данным курсом, методикой решения задач и изучения теоретических знаний, поиском прикладных возможностей. Введение теории вероятностей в стандарты второго поколения усилили актуальность сформированного объема знаний, понимания важности вероятностной культуры человека, необходимости поиска методических и дидактических «изюминок».
Практическая значимость и новизна представляемого опыта работы заключаются в его авторском эксклюзиве систематического использования графов при решении задач, в методической и дидактической метапредметности формирования информационной культуры. Программные требования стандартов нашли продолжение в проектной и исследовательской деятельности учителя и учащихся. Открытость опыта подтверждается работающим тематическим сайтом, то есть возможностью многократной трансляции и интерпретации.
На страницах данной работы представлен опыт программно-содержательного конструирования стохастической линии математики вообще и теории вероятностей в частности, предложены методические советы по использованию методических и дидактических приемов изучения теории и применения на практике. Особенностью авторского опыта освоения курса теории вероятностей является изложение предмета с систематическим использованием графов, что делает более наглядным и доступным рассматриваемый материал. Предложены варианты использования современных интерактивных средств обучения и контроля знаний: интерактивная доска, системы электронного контроля знаний. В приложениях представлены конкретные результаты совместной работы учителя и учеников гимназии № 8 им.Л.М. Марасиновой.
Обязательный минимум содержания образования предопределяет стандарт, некоторую рамку теоретических и практических знаний и умений. С этой точки зрения содержание раздела Вероятность и статистика предполагает изучение следующих вопросов: Представление данных, их числовые характеристики. Таблицы и диаграммы. Случайный выбор, выборочные исследования. Интерпретация статистических данных и их характеристик. Случайные события и вероятность. Вычисление вероятностей. Перебор вариантов и элементы комбинаторики. Испытания Бернулли. Случайные величины и их характеристики. Частота и вероятность. Закон больших чисел. Оценка вероятностей наступления событий в простейших практических ситуациях.
Актуальной становится проблема выбора соответствующего учебно-методического комплекса, наиболее полно сопровождающего образовательный процесс, и отбор тех дидактических приемов, которые позволят оптимально реализовать требуемые задачи стохастического образования. Подробный содержательный анализ действующих на момент 2007 года УМК, представлен на страницах авторского тематического сайта (Приложение 2).
Анализ утвержденных учебно-методических комплексов показывает, что обязательное освоение стохастической линии математики в основной школе и на 3 ступени обучения, только учебник Г.В. Дорофеева и И.Ф. Шарыгина предполагает в следующем варианте:
Углубленное изучение предмета (по учебнику Н.Я. Виленкина для классов с углубленным изучением предмета) предполагает следующие программные требования к содержанию:
Профильный уровень математики предполагает изучение данных разделов по учебнику А.Г. Мордковича в 10 классе.
Чтобы компенсировать содержательный недостаток учебных пособий, авторы некоторых из них разработали дополнительные параграфы к курсу алгебры 7-9 классов, предлагая и поурочное планирование: А.Г. Мордкович и П.В. Семенов; М.В. Ткачева и Н.Е. Федорова [6, 8] «Элементы статистики и вероятность»
К другим учебно-методическим комплексам таких пособий пока не разработано. Выход для учителя – практика из создавшейся ситуации заключается в авторской разработке рабочей программы, элективного курса с учетом всех возникших противоречий по введению стохастической линии в курс средней школы и предлагаемых путей их разрешения.
Учитывая, что ни одна наука не должна осваиваться учениками обособленно, в отрыве друг от друга, мною была предпринята попытка найти содержательное взаимопроникновение геометрии, алгебры, арифметики, информатики и стохастики.
Фундирование раздела математики основной школы
«Элементы логики, комбинаторики, статистики и теории вероятностей» (45 часов)
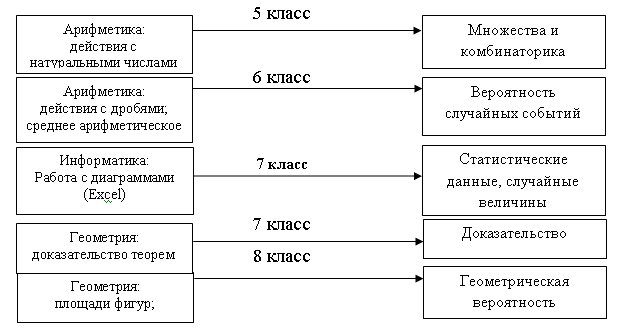
Фундирование раздела математики средней школы
«Элементы комбинаторики, статистики, теории вероятностей»
20 часов – база, 25 часов – проф. гуманитарный, 20 часов – проф. математический

Таким образом, творчески выстраивая рабочую программу, учитель имеет возможность использовать образовательную базу других разделов или науки, создавая условия для метапредметности каждого вопроса. Но творчество учителя на этом не завершается. Гораздо большие возможности для проявления авторства и, соответственно, творчества учителя математики появляется с выбором дидактических приемов введения и дальнейшего применения основных понятий курса стохастики. Конструктивно авторское видение спирали фундирования понятий теории вероятностей в средней школе в совокупности с дополнительным образованием выглядит следующим образом
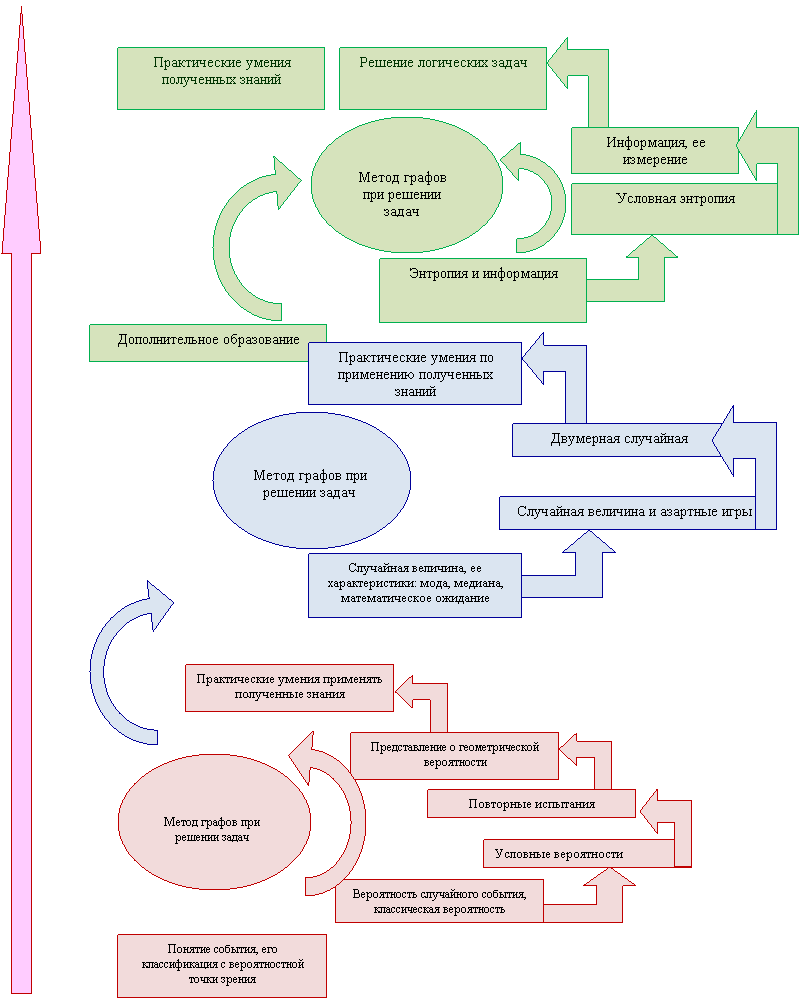
Данный раздел работы - необходимый содержательный минимум, которым должен владеть педагог, приступающий к освоению и преподаванию курса теория вероятностей.
Любая точная наука изучает не сами явления, протекающие в природе, в обществе, а их математические модели, т. е. описание явлений при помощи набора строго определенных символов и операций над ними. При этом для построения математической модели реального явления во многих случаях достаточно учитывать только основные факторы, закономерности, которые позволяют предвидеть результат опыта (наблюдения, эксперимента) по его заданным начальным условиям. Однако есть множество задач, для решения которых приходится учитывать и случайные факторы, придающие исходу опыта элемент неопределенности.
Теория вероятностей - математическая наука, изучающая закономерности, присущие массовым случайным явлениям. При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы. То есть теория вероятностей рассматривает не сами реальные явления, а их упрощенные схемы - математические модели. Предметом теории вероятностей являются математические модели случайных явлений (событий). При этом под случайным явлением понимают явление, предсказать исход которого невозможно (при неоднократном воспроизведении одного и того же опыта оно протекает каждый раз несколько по-иному). Примеры случайных явлений: выпадение герба при подбрасывании монеты, выигрыш по купленному лотерейному билету, результат измерения какой-либо величины, длительность работы телевизора и т. п. Цель теории вероятностей - осуществление прогноза в области случайных явлений, влияние на ход этих явлений, контроль их, ограничение сферы действия случайности. В настоящее время нет практически ни одной области науки, в которой в той или иной степени не применялись бы вероятностные методы [7, с.9].
Случайным событием (или просто: событием) называется любой исход опыта, который может произойти или не произойти. События обозначаются, как правило, заглавными буквами латинского алфавита: А, В, С, ... .
Если появление одного события в единичном испытании исключает появление другого, такие события называются несовместными. Если при рассмотрении группы событий может произойти только одно из них, то его называют единственно возможным. Наибольшее внимание математиков в течение нескольких столетий привлекают равновозможные события (выпадение одной из граней кубика) [4, с.31].
Примеры: а) при подбрасывании игральной кости пространство элементарных событий П состоит из шести точек: П={1,2,3,4,5,6}; б) подбрасываем монету два раза подряд, тогда П={ГГ, ГР, РГ, РР}, где Г - «герб», Р - «решетка» и общее число исходов (мощность П) |П| = 4; в) подбрасываем монету до первого появления «герба», тогда П={Г, РГ, РРГ, РРРГ,...}. В этом случае П называется дискретным пространством элементарных событий.
Обычно интересуются не тем, какой конкретно исход имеет место в результате испытания, а тем, принадлежит ли исход тому или иному подмножеству всех исходов. Все те подмножества А, для которых по условиям эксперимента возможен ответ одного из двух типов: «исход принадлежит А» или «исход не принадлежит А», будем называть событиями [2, с.27]. В примере б) множество А={ГГ, ГР, РГ} является событием, состоящим в том, что выпадает по крайней мере один «герб». Событие А состоит из трех элементарных исходов пространства П, поэтому |А| = 3.
Суммой двух событий А
и В называется событие С=А+В, состоящее в выполнении события А или события В.
Произведением событий А и В называется событие D=A·B, состоящее в
совместном исполнении события А и события В. Противоположным по отношению к
событию А называется событие ![]() , состоящее
в непоявлении А и, значит, дополняющее его до П. Если каждое появление события А
сопровождается появлением В, то пишут A
, состоящее
в непоявлении А и, значит, дополняющее его до П. Если каждое появление события А
сопровождается появлением В, то пишут A![]() В
и говорят, что А предшествует В или А влечет за собой В.
В
и говорят, что А предшествует В или А влечет за собой В.
Исторически первым определением понятия вероятности является то определение, которое в настоящее время принято называть классическим, или, классической вероятностью: классической вероятностью события А называется отношение числа благоприятных исходов (обязательно наступивших) к общему числу несовместных единственно возможных и равновозможных исходов [3, с.12]: Р(А) = m/n, где m – число исходов, благоприятных для события А; n- общее число несовместных единственно возможных и равновозможных исходов. С точки зрения значения случайности все события можно классифицировать следующим образом:

Несколько событий называются совместными, если появление одного из них в единичном испытании не исключает появления других событий в этом же испытании. В противном случае события называются несовместными.
Два события называются зависимыми, если вероятность одного события зависит от появления или непоявления другого. Два события называются независимыми, если вероятность одного события не зависит от появления или непоявления другого. Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация остальных событий есть события независимые. Несколько событий называются попарно независимыми, если любые два из этих событий независимы.
Требование независимости в совокупности сильнее требования попарной независимости. Это значит, что несколько событий могут являться попарно независимыми, но при этом они не будут независимыми в совокупности. Если же несколько событий независимы в совокупности, то из этого следует их попарная независимость. В связи с тем, что в дальнейшем часто нужно будет рассматривать вероятности одних событий в зависимости от появления или непоявления других, то необходимо ввести еще одно понятие.
Условной вероятностью РА(В) называется вероятность события В, вычисленная при условии, что событие А уже произошло.
Одним из важнейших понятий теории вероятностей (наряду со случайным событием и вероятностью) является понятие случайной величины.
Под случайной величиной понимают величину, которая в результате опыта принимает то или иное значение, причем неизвестно заранее, какое именно. Примерами случайной величины могут служить: 1) X — число очков, появляющихся при бросании игральной кости; 2) Y — число выстрелов до первого попадания в цель; 3) Z — время безотказной работы прибора и т.п. Случайная величина, принимающая конечное или счетное множество значений, называется дискретной. Если же множество возможных значений случайной величины несчетно, то такая величина называется непрерывной.
То есть дискретная случайная величина принимает отдельные изолированные друг от друга значения, а непрерывная случайная величина может принимать любые значения из некоторого промежутка (например, значения на отрезке, на всей числовой прямой и т.д.). Случайные величины X и Y (примеры 1) и 2)) являются дискретными. Случайная величина Z (пример 3)) является непрерывной: ее возможные значения принадлежат промежутку [0, t), где t > 0, правая граница не определена. Отметим, что рассматриваются также случайные величины смешанного типа.
Дадим теперь строгое определение случайной величины, исходя из теоретико-множественной трактовки основных понятий теории вероятностей. Случайной величиной X называется числовая функция, определенная на пространстве элементарных событий П, которая каждому элементарному событию w ставит в соответствие число Х(w), т.е. X = X(w) [2, с.63]. Пример. Опыт состоит в бросании монеты 2 раза. Можно рассмотреть случайное событие – появление герба и случайную величину X — число появлений герба.
Основными характеристиками случайной величины являются характеристики положения (математическое ожидание, мода, медиана) и характеристики рассеивания (дисперсия, среднеквадратичное отклонение) [6, с.65].
Математическое ожидание вычисляется по формуле М[X]=Σxipi и характеризует среднее значение случайной величины.
Мода (М0) – это такое значение случайной величины, для которого соответствующее значение вероятности максимально.
Медианой дискретной случайной величины (Ме) называется такое значение хk в ряду возможных значений случайной величины, которые она принимает с определенными значениями вероятностей, что приблизительно равновероятно закончится ли процесс до хk или продолжится после него.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D[Х]=М(Х-М[Х])2 = М[Х2]-М2[Х].
Среднеквадратическим
отклонением случайной величины Х называют положительное значение квадратного
корня из дисперсии: σ[Х]=![]()
![]() .
.
Задачи, связанные с понятиями случайного события и случайной величины, эффективно рассматривать через графическую иллюстрацию с применением вероятностного графа, на ребрах которого надписаны соответствующие значения вероятностей [2].
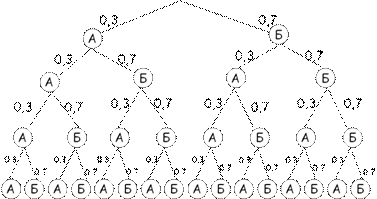
Ответ: пропорционально вероятности выигрыша.
Любое правило (таблица, функция, график),
X |
x1 |
x2 |
..... |
xn |
..... |
P |
p1 |
p2 |
..... |
pn |
..... |
позволяющее находить вероятности произвольных событий, в
частности, указывающее вероятности отдельных значений случайной величины или
множества этих значений, называется законом распределения случайной величины
(или просто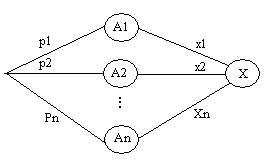 : распределением). Про случайную величину говорят, что «она
подчиняется данному закону распределения» – соотношению, устанавливающему связь
между возможными значениями случайной величины и соответствующими вероятностями. Закон распределения дискретной случайной величины обычно задается в виде
таблицы, где в верхней строке записаны значения случайной величины, а в нижней –
под каждым хi – соответствующие вероятности рi
: распределением). Про случайную величину говорят, что «она
подчиняется данному закону распределения» – соотношению, устанавливающему связь
между возможными значениями случайной величины и соответствующими вероятностями. Закон распределения дискретной случайной величины обычно задается в виде
таблицы, где в верхней строке записаны значения случайной величины, а в нижней –
под каждым хi – соответствующие вероятности рi
Закон распределения может иметь геометрическую иллюстрацию в виде графа распределения [6].
Еще раз обозначим обязательный минимум содержания соответствующего раздела, записанный в новых стандартах школьного математического образования:
Основная школа: Понятия и примеры случайных событий. Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.
Старшая школа: Элементарные и сложные события. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов. Поочередный и одновременный выбор нескольких элементов из конечного множества.
Знакомство с вероятностно-статистическим материалом целесообразно начинать с трех важнейших понятий, предваряющих определение вероятности: случайный опыт, случайное событие, элементарный исход. Со случайными событиями знакомство можно начинать уже в 5 классе, так как в этом возрасте закладываются основы вероятностной интуиции, позволяющие впоследствии усвоить формальные методы вычисления вероятностей. В этот период ученики должны научиться выделять невозможные и достоверные события.
В 6-7 классах появляется понятие случайного эксперимента, в контексте которого рассматривается любое случайное событие, формируется представление о его возможных исходах. Особое внимание следует уделить обсуждению «элементарности» исходов, поскольку непонимание этого признака повлечет дальше неизбежные ошибки при вычислении вероятностей. Принципиальным моментом этого раздела является переход от словесного описания событий и экспериментов к теоретико-множественному. На этом этапе ученики должны уметь:
Классический и геометрический подход к определению вероятности должны рассматриваться как частные случаи вероятностных моделей, в которых это число удается вычислить (предсказать) без проведения опыта. Вероятность появляется как универсальная количественная мера возможности осуществления случайных событий, а все частные формулы для ее подсчета служат лишь для вычисления этой меры в определенном круге ситуаций.
При изучении этого раздела полезными оказываются уроки с применением мультимедийных средств, электронные лаборатории, позволяющие в считанные секунды смоделировать тысячи случайных экспериментов, наблюдая при этом за динамикой изменения частот и их приближением к вероятностям случайных исходов и событий.
Открыв формулу Лапласа Р(А) = m/n, ученики включаются в процесс не только экспериментального поиска ответа на вопрос о вероятности какого-либо события, но и приступают к вычислению. Важно сформировать у учеников понимание условия применимости формулы Лапласа: опыт должен иметь конечное число равновозможных исходов.
В результате нескольких лет работы по освоению практики решения задач по теории вероятностей составлены алгоритмы классического (комбинаторного ) способа и способа с помощью вероятностных графов:
|
Классический способ |
Способ решения с помощью вероятностного графа |
|
Описание возможных исходов опыта, их кодирование и перечисление (полное или частичное) |
Формулировка события и его благоприятного исхода |
|
Обоснование равновозможности перечисленных исходов |
Изображение графа – модели конкретной задачи. |
|
Подсчет общего числа исходов опыта n: прямой подсчет, с помощью комбинаторных формул |
Выбор благоприятных исходов |
|
Описание благоприятных исходов для события А, их перечисление |
Заполнение значений вероятностей над каждым ребром графа |
|
Подсчет благоприятных исходов |
Вычисление общей вероятности |
|
Вычисление вероятности по формуле Лапласа |
|
Решение задач обоими способами представлено в следующей главе работы.
Получив ответ, необходимо обсудить с учениками его реальный смысл, привести частотную интерпретацию. Полезно выяснить, совпадает ли полученная величина с интуитивным представлением учеников о вероятности, удовлетворяет ли основным свойствам.
Для тематического и периодического контроля (особенно, когда широко применяется тестирование) в последние годы все шире применяется система интерактивного голосования и опроса Hitachi Verdict и система Votum. Преимущества электронного тестирования перед традиционными формами очевидны: не нужно тратить время на проверку контрольных – результаты обрабатываются автоматически, накапливается первичная статистика, что освобождает преподавателя от рутинной работы. Результаты контрольной можно увидеть сразу после окончания опроса, а детализированные отчеты позволяют выявить не только уровень знаний каждого ученика, но и моментально оценить, какие темы вызывают наибольшую сложность. Особенно это актуально при столь незначительном учебном времени, которое отводится на изучение Теории вероятностей. Для контроля разработаны тематические тесты оперативного контроля (Приложение 3) и итогового контроля, различные кроссворды (Приложение 1) , и собственно контрольные (Приложение 4) и зачетные работы
Среди приложений к работе можно найти разработки урока, элективного занятия, технологические карты темы и отдельных уроков (Приложение 5, Приложение 6, Приложение 7, Приложение 8, Приложение 9).
Отличительной особенностью авторского подхода к ведению курса теории вероятностей является изложение предмета с систематическим использованием графов, что делает изучаемый материал более наглядным и доступным.
Графом называется два множества с отношением инцидентности между их элементами, называемыми вершинами и ребрами. Любое ребро связано не более чем с двумя вершинами. [2, с.26]
Деревом называется связный граф без циклов. Очень важное понятие для подхода изложения теории вероятностей. При помощи дерева удобно изображать исходы того или иного испытания. [2, с.27]
Граф называется вероятностным, если рядом с каждым его ребром записать соответствующую вероятность. [2, с.29]
Вероятность события вычисляется путем сложения вероятностей благоприятного исхода, которую в свою очередь определяем произведением вероятностей каждого ребра, соответствующего этому благоприятному событию.
Если вернуться к анализу имеющихся учебных пособий, то в учебнике Дорофеева, учебных пособиях, Мордковича вводится понятие «дерево исходов», «дерево возможных вариантов». В учебном пособии Ткачевой и Федоровой вводится понятие графа для подсчета вариантов. Но при изучении тем «Случайные события» и «Случайные величины» возможности эффективного инструмента - вероятностного графа - для решения соответствующего круга задач даже не предполагается, что опять ложится в основу профессиональной инициативы учителя.
Задача 1. Пусть два брата считают до числа, которое оказалось суммой «выброшенных» пальцев одной руки каждого. Тот, на котором остановился счет, выходит, а оставшийся убирает квартиру. Играет ли роль, с кого начинать счет?
Рассмотрим решение задачи двумя способами.
1 способ – комбинаторный.
Очевидно, что выбор таким образом дежурного является случайным. Обратим внимание на то, что первый, с кого начинается счет, не убирает квартиру, если сумма «выброшенных» пальцев окажется нечетной, а второй – если четной.
I игрок:
3 = 1+2 = 2+1
5 = 1+4 = 4+1 = 2+3 = 3+2
7 = 2+5 = 5+2 = 3+4 = 4+3
9 = 4+5 = 5+4
II игрок: 2= 1+1
4 = 1+3 = 3+1 = 2+2
6 = 1+5 = 5+1 = 2+4 = 4+2 =3+3
8 = 3+5 = 5+3 = 4 +4
10 =5+5
Для первого игрока получили 12 благоприятных ему исходов, а для второго 13, следовательно, при игре в «считалки» предпочтительней стоять вторым.
2 способ. Составим вероятностное дерево исходов:

Р2 > Р1 и, следовательно, при игре в «считалки» выгодней стоять вторым. В последнем решении использованы интерпретации на графах теорем сложения и умножения вероятностей:
P (A+B) = P (A) + P (B) и в частности
P (A+B) =P (A) + P (B), если A и B – несовместные события
P (A*B) = P (A)*P (B), если A и B – независимые события.
Рассмотрим двумя способами решение одной из классических задач теории вероятностей – задачи Гюйгенса.
Задача Гюйгенса: В урне 2 белых и 4 черных шара. Один азартный человек держит пари с другим, что среди вынутых 3 шаров будет ровно 1 белый. В каком отношении находятся шансы спорящих.
Решение:
1 способ. Традиционное решение - комбинаторное:
Испытание Ω = {вынимание шаров}, событие А, благоприятствующее одному из спорящих: А ={достать ровно один белый шар}.
Учитывая, что порядок вынимаемых трех шаров не важен, то
![]()
Один белый шар можно достать
в ![]() случаев, а
2 черных -
случаев, а
2 черных - ![]() . По
основному правилу комбинаторики
. По
основному правилу комбинаторики ![]() . Отсюда
. Отсюда ![]() , а по
свойству вероятности P(
, а по
свойству вероятности P(![]() )=1-P(A)=
)=1-P(A)=![]() . Cледовательно,
P(A): P(
. Cледовательно,
P(A): P(![]() )=3:2
)=3:2
Ответ: шансы спорящих находятся как 3:2, т.е. скорее так и будет: среди 3 вынутых шаров будет ровно 1 белый.
2 способ. Использование вероятностного графа.
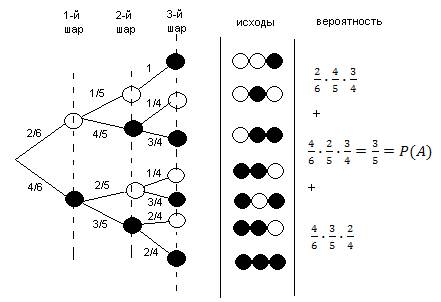
Возможность решения задач по теории вероятностей с помощью графов появляется уже в 6 классе, в процессе изучения темы «Обыкновенные дроби. Арифметические действия с обыкновенными дробями». Значит, к этому моменту можно ввести понятие случайных, достоверных и недостоверных событий, показать простейшие задачи, решаемые с помощью вероятностного графа.
Практика показывает, что трудностей на данном этапе у учащихся не возникает. Иллюстрация с помощью графа делает данный процесс творческим и наглядным. При этом формируется практический навык анализа происходящего, сравнение и выбор. Причем, графический метод не требует знания формул комбинаторики и способствует развитию аналитических навыков:
Решение: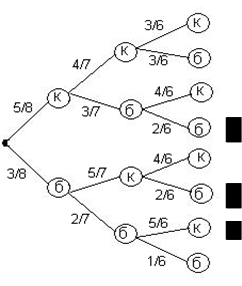
А={1 красный цвет} Р(А)=![]()
На данной задаче можно построить еще ряд вопросов, ответы на которые легко найти, используя данный граф: B={2 красных}, С={3 одинаковых цвета}и т.д.
Ответ: P(A)=![]()
В наборе содержатся кегли
4 цветов: белые, красные, зеленые и желтые. Какова вероятность того, что
среди 3 выбранных кеглей из набора в 36 кеглей будет только одна  белого
цвета?
белого
цвета?
Решение: A={только одна кегля белого цвета}
Аналогично предыдущей задаче при построении графа учитываем то, что при вынимании 1 кегли определенного цвета их количество уменьшается. В данном испытании благоприятным исходом считается кегля белого цвета (их в наборе 9), неблагоприятным все остальные, независимо от цвета.
P(A)=![]()
Ответ: P(A)![]()
Мои ученики предложили рациональный подход: строим граф, определяем благоприятные исходы и вероятности надписываем над ребрами графа только при благоприятных исходах, что значительно экономит время, делает решение более осознанным (зачем делать лишнюю работу). Они правы, но тогда число дополнительных вопросов для быстрого ответа по готовому графу будет ограничено. Можно предложить дозаполнить граф дома, а потом при необходимости к нему вернуться.
После решения 2 задач (любых) при формировании вероятностной культуры, целесообразно задавать вопросы: что более вероятно…, какой ответ соответствует большей вероятности и т.д. с точки зрения математики ученики сравнивают полученные ответы, с точки зрения теории вероятностей они формируют четкое понимание, что максимальная вероятность = 1, более вероятны события, вероятность наступления которых близка именно к этому значению. В двух предыдущих задачах обе вероятности меньше 50%. Вероятность события во второй задаче больше, чем в первой, но обе они свидетельствуют одинаково о маловероятности наступления данного события.
На трех карточках
написаны цифры 1,2 или 3. Случайным образом из этого набора выбирают
последовательно по одной карточке и кладут в ряд, образуя трехзначное число.
Какова вероятность того, что образуется число: 1). 123, 2). 213, 3) 132, 4)
231, 5). 312, 6). 321. [6, с.47]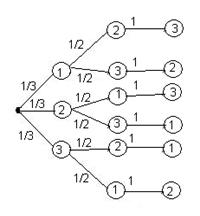
Решение: 1) A={число
123} P(A)=![]()
Анализируя граф, несложно заметить, что любое другое число получается именно с такой же вероятностью.
Ответ: P(A)=![]()
Данную задачу можно несколько усложнить с точки зрения теории вероятностей, если какую-нибудь карточку предложить дважды. Например, карточка «2». То есть из 4 карточек составить указанные числа.
На каждой из двух
карточек написана цифра 1, а на третьей – цифра 2. Эти три карточки
перемешиваются и случайным образом выкладываются в ряд. Какие числа при этом
могут получиться и найдите вероятность получения каждого из них. [6, .47]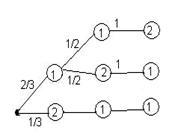
Решение:
Очередность вынимания той или иной цифры и , соответственно, составление того или иного числа несложно отразить на графе, рассуждая логически: первой цифрой может оказаться и «1» и «2», но каждая со своей долей вероятности. Дальнейшие сценарии определяются аналогично и фиксируются графом. Определив вероятности, произведя необходимые вычисления, получаем ответ: различных чисел может быть только три и вероятность каждого соответственно равна:
P(112)=![]() ;
P(121)=
;
P(121)=![]() ;
P(211)=
;
P(211)= ![]()
В ящике находятся 2 белых
и 2 черных шара. Наугад вынимают 2 шара. Какие комбинации могут получиться и
найти вероятность каждой из них. [6, с.48]
Решение:
P(бб) =![]() ;
P(бч) =
;
P(бч) =![]() ;
P(чб) =
;
P(чб) =![]() ;
P(чч) =
;
P(чч) =![]()
Применение полученных знаний и первичных навыков может быть осуществлено при решении следующей задачи в различных (соответствующих) разделах математики.
Из карточек с числами 1,2,3,4,5 выбирают три. Найдите вероятность следующих событий:
1). Существует прямоугольный треугольник с такими сторонами;
2). Существует произвольный треугольник с такими сторонами;
3). Произведение этих чисел оканчивается на ноль;
4). Сумма этих чисел меньше 10.
Решение. Для всех данных (и
вообще возможных) задач достаточно построить ОДИН граф, далее провести анализ
выборки по условию конкретной задачи. Подсчет возможных комбинаций трех чисел из
пяти можно провести и комбинаторным способом ![]() .
Построение данного графа, в итоге которого будет 60 комбинаций – дело
трудоемкое, но для решения нескольких задач на одном графе оправдывает
подготовительные задачи.
.
Построение данного графа, в итоге которого будет 60 комбинаций – дело
трудоемкое, но для решения нескольких задач на одном графе оправдывает
подготовительные задачи.
1). Р(А) = 6/60; 2). Р(А) = 17/60; 3). Р(А) = 27/60; 4). Р(А) = 34/60
Мои ученики предложили использовать для этого электронные таблицы Excel.
Данную задачу можно несколько усложнить с точки зрения теории вероятностей, если какую-нибудь карточку предложить дважды.
Итак, достаточно оптимально происходит решение задач на подсчет вероятности случайных событий с помощью вероятностного графа, что также позволяет не только решать данные задачи, но и моделировать новые, изменяя условие или вопрос.
С помощью графов успешно решаются задачи и других разделов теории вероятностей. Напомним, что условной вероятностью события А при условии, что событие В произошло, называется отношение Р (А*В) / Р (В)
Слово «МАТЕМАТИКА» разделено на отдельные буквы, из них произвольным образом отбираются и выкладываются по порядку четыре буквы. Какова вероятность получения слова «МАМА»?
Решение. Пусть событие А={получить слово «МАМА»}. Возьмем в дереве испытаний ветвь, соответствующую событию А, и найдем ее вес:
 |
При изучении темы «Случайные величины» вводятся основные характеристики случайной величины – математическое ожидание, мода, медиана, вычисление которых с помощью графов также более наглядно и структурировано.
Какую игру следует
выбрать: с призом в 8 рублей за выпадение, по крайней мере, одного герба
(А), или с призом в 16 рублей за выпадение ровно двух гербов (В) при трех
подбрасываниях монет. [1, с.68] 
Решение:
Р(А) = 7*1/23=7/8 M[A] = 8*7/8=7 P(B) = 3*1/23=3/8 M[B] = 16*3/8=6
Вывод: выгоднее выбрать игру с призом в 8 рублей
Большие возможности для
анализа условия задачи и понимания сути решения дает применение графов при
решении задач, связанных с выработкой стратегии игры. Несложные вычисления
позволяют определить наиболее выигрышную тактику игрока.
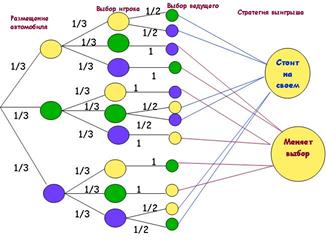
Задача Монти – Холла [1, с.39]. (американская Теле игра «Заключим пари»)
За одной из трех дверей находится приз – автомобиль, за двумя другими – пустая комната. Играющему предлагается открыть одну из трех дверей.
Игра проходит в три этапа:
Р(А)=![]() Р(Б) =
Р(Б) =![]()
Оптимальность образовательного процесса при решении подобных задач достигается благодаря применению интерактивной доски. Однажды созданный и разобранный вероятностный граф в компьютерной программе может быть многократно проанализирован в соответствии с вопросом задачи, и сделанная выборка нужных ситуаций позволяет сэкономить время на уроке, посвятив его разбору множества вопросов, а не вырисовыванию многоструктурного графа.
Как и многие изучаемые в
школьном курсе математики темы предполагают возможность изучения дополнительных
разделов через элективные курсы, факультативы, научно-исследовательскую
деятельность, так и «Теория вероятностей и математическая статистика» может
иметь продолжение и возможность интеграции с обязательными темами изучения в
средней школе. Знакомство учащихся с нетрадиционными вопросами теории
вероятностей позволяет увидеть возможности продолжения понятия вероятности и их
применения для решения школьных логических задач, рассмотреть практическое
применение некоторых вопросов программного материала. Одним из таких вопросов
является решение логических задач с помощью понятия энтропии.
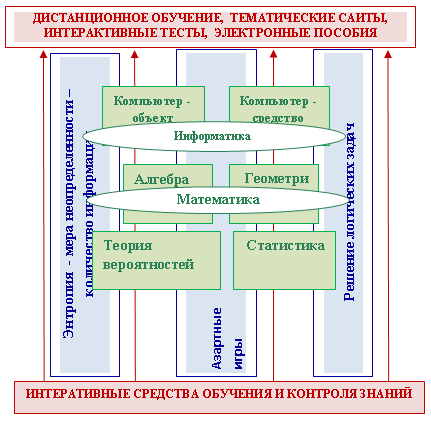
Изучая теорию вероятностей, статистику важно показать ученикам применимость получаемых знаний. Построенная таким образом система позволяет это сделать через метапредметные модули, реализуемые на уроках, в проектной деятельности.
В основной школе учащиеся знакомятся с понятием графа (дерева возможных вариантов), в рамках элективных курсов могут рассматривать (рассматривают) логические задачи на выделение элемента множества (задачи на взвешивание, угадывание задуманного, о лжецах) и их решение с помощью графов и логических рассуждений. Но при этом остается открытым вопрос о минимально возможном числе взвешиваний или вопросов. Учащиеся не владеют математическими знаниями для решения подобных задач с целью получения однозначно неопровержимого ответа. Конечно, при построении графов развивается логическое мышление, внимание, формируется умение выдвигать гипотезы, но поиск возможных числовых ответов порой не может убедить, что это «наименьшее».
Введение в средней школе понятия логарифма, и его свойств, интеграция данной темы с вопросами теории вероятностей, рассмотренными в основной школе, позволяет не только дать однозначный ответ на вопрос задачи о наименьшем количестве взвешиваний (вопросов), но и продемонстрировать практическое приложение понятия логарифма.
Все это раскрывает тема «Энтропия и информация», которая не является общепринятым материалом курса «Теория вероятностей», но способствует установить аналогии новых результатов с ранее рассматриваемыми. Удачно занятия по данной теме проводить параллельно с изучением темы «Логарифмы», но возможно более позднее обращение к теме «Энтропия и информация» чем изучение логарифмов. В таком случае – «Энтропия и информация» - модуль (14 часов) целостного метапредметного элективного предмета «В мире информации», рассчитанного на 34 часа. Первый подход – практическое применение изучаемого, второй подход и практическое применение изученного и его повторение. Возможно, при достаточно высоком уровне подготовки обучающихся данный курс (14 часов) предложить уже в 9 классе, объяснив понятие логарифма и предоставив информацию по его простейшим свойствам. В моей практике осуществлены все три подхода.
Цели курса «Энтропия и информация»
Для достижения поставленных целей необходимо решить следующие задачи:
В результате освоения данного курса ученик должен научиться:
Актуальность программы определяется необходимостью осознания учащимися связи теории вероятностей и алгебры с практикой жизни. Курс предполагает овладение широким понятийным аппаратом, знакомство с различными логическими структурами определений, развитие умений подводить объект под понятие, применять определения в процессе рассуждений. Теоретический и практический материал курса в силу своей компактности, информативности предоставляет возможности школьникам быстрее и с меньшими трудностями проследить процесс обобщения понятий. Во многом этому способствует авторский мультимедийный продукт.
Усвоению знаний должно способствовать развитие умения анализировать, выявлять закономерности, обобщать, логически излагать свои мысли, ставить и разрешать проблемы. Курс должен помочь школьникам овладеть способами исследовательской деятельности, стать фактором формирования творческого мышления. Как методическое пособие можно использовать тематический буклет педагога (Приложение 12).
Общие принципы отбора содержания материала:
Системность содержания достигается логикой развертывания учебного материала таким образом, что изучение всех последующих тем обеспечивается предыдущими, а между частными и общими знаниями прослеживаются связи.
Организация учебной работы предусматривает:
Учебно-тематический план: Каждое занятие по 2 часа.
Итого: 14 часов (можно увеличить количество часов на решение логических задач)
Основным принципом учебно – исследовательской работы является учет образовательных потребностей ученика, выходящих за рамки того или иного предмета, овладение методами самостоятельного научного исследования. Под исследовательской деятельностью учащихся сегодня понимается такая форма организации учебно-воспитательной работы, которая связана с решением учащимися творческой, исследовательской задачи с заранее неизвестным для них, в первую очередь, результатом в различных областях науки, техники, искусства и предполагающая наличие основных этапов характерных для научного исследования:
Исследовательская работа предполагает индивидуальный темп и способ продвижения, обеспечивая при этом достаточно высокий уровень знания. При подборе темы полезно обратить внимание на смежные области знания: иногда на стыке двух научных дисциплин, например экономики и математики, можно найти такие темы, которые как бы забыты и той и другой отраслями науки, но имеют определенные исследовательские перспективы и интересны для ребят.
Система действий учителя и учащихся при выборе и утверждении тем предполагаемых исследований может быть следующей:
|
Учитель отбирает возможные темы |
Ученики самостоятельно подбирают темы |
|
Учитель предлагает учащимся возможные темы |
Учащиеся обсуждают и принимают решение |
|
Учитель участвует в обсуждении тем, предложенных учащимися |
Ученики предлагают для обсуждения самостоятельно подобранные темы |
|
Учитель организует совместное утверждение тем |
Ученики принимают решение. |
Раздел математики Теория вероятностей также предполагает включение обучающихся в научно-исследовательскую деятельность, реализацию проектов, подготовку тематических сообщений.
Информационную ценность имеет тематическое сообщение учеников «Из истории теории вероятностей» (Приложение 14), и сообщение учителя «Теория вероятностей», сопровождающаяся презентацией (Приложение 7).
Метапредметный характер имеет проект обучающихся «Информация и логические задачи» (Приложение 15), в рамках которого рассматривается методика решения задач на взвешивание, на угадывание. Демонстрируется метод половинного деления, дающий наиболее оптимальный способ решения.
Среди всех проектов моих учеников самым ярким, результативным, практико-ориентированным является проект «Теория вероятностей и жизнь» (запуск проекта - Приложение 16), направленный не только на метапредметность изучаемой науки, но и на демонстрацию роли теории вероятностей для формирования устойчивого отношения к азартным играм, лежащим в основе появления науки, и являющиеся определенным пороком мира взрослых. Результатом данного проекта стали тематические буклеты (Приложение 17), презентации (Приложение 18, Приложение 19), исследовательские работы (Приложение 20).
Проект рассчитан на учащихся 9-11 классов, является краткосрочным, информационно-исследовательским, основан на изучении раздела математики Теория вероятностей. В ходе реализации проекта, который может быть запущен еще до изучения данной темы в рамках воспитательного мероприятия через презентацию учителя «Дети в окружении пороков взрослых», учащиеся не только познакомятся с основными понятиями и формулами теории вероятностей, но и увидят, как теория вероятностей помогает предостеречь от воздействия азартных игр на незадачливых игроманов. Именно теория вероятностей помогает определить размер начальной ставки в игре, чтобы она стала безобидной или благоприятной, поможет распределить сделанные ставки, если игра завершена досрочно, и, вообще, подскажет, стоит ли играть, если его величество Случаем в организованных заведениях для игроманов руководит его величество Человек (знающий основы теории вероятностей и рассчитавший свой успех). Кроме воспитательного значения, проект имеет образовательный потенциал, так как демонстрирует прикладное значение изучаемого раздела математики.
У. Уивер пишет: «Теория вероятностей и статистика — две важные области, неразрывно связанные с нашей повседневной деятельностью. Мир промышленности, страховые компании в большой степени являются должниками вероятностных законов. Сама физика имеет существенно вероятностную природу; такова же в основе своей и биология. Между тем, несмотря на эту важность, универсальный характер теории вероятностей и статистики все еще не стал общепринятым среди деятелей образования» [9, с. 376-377].
Изучая случайные события и явления, осуществляя поиск закономерностей не только в математике и других науках, актуальными становятся вопросы о степени случайности, о возможностях, которые могут снизить степень случайности события, переводя его в разряд реальности бытия. Именно, исходя из этого, представленный авторский опыт введения теории вероятности становится актуальным, предполагающим дальнейшее совершенство.